Fazer contas de cabeça é uma habilidade que estamos perdendo com o passar do tempo, e isso ninguém pode discordar. Somos muito piores em fazer contas do que nossos pais, por exemplo, já que eles foram treinados para a tarefa em uma época em que não havia qualquer recurso extra que facilitasse os processos matemáticos. Já nós, temos um parceiro que resolve todo o trabalho duro em milésimos de segundo: a calculadora.
A configuração básica do dispositivo é simples. 10 botões para os números, 4 botões para as operações e 1 botão para exibir o resultado do cálculo. É só apertar a sequência de teclas desejada e pronto, o resultado sai certinho. Quem duvidar pode fazer na mão para confirmar, se conseguir, é claro.
Mas, alguma vez, você já parou para pensar no que acontece ali dentro e faz com que os cálculos sejam executados corretamente? Pois é, eu já. A resposta deu um post, confere aí.
Como chegamos nas calculadoras de bolso
Como você, talvez, já suspeite, toda a mágica decorre de um pequeno componente embarcado nas calculadoras chamado circuito integrado, ou, MICROCHIP, como é popularmente conhecido. Mas não posso só chegar aqui e despejar a teoria, ainda mais que as calculadoras têm uma história bastante interessante. Aproveito para contá-la agora.
Bom, primeiramente enfatizo um ponto: não é que não existissem calculadoras antes dos microchips, afinal tínhamos o ábaco há milênios e tantos outros exemplos de máquinas mecânicas que fazem cálculos na história da ciência, porém, elas eram lentas, raras e passíveis de erros, muitos erros, afinal, seu resultado dependia de como os passos intermediários eram operadas por humanos. Tá certo que as de hoje também são assim, mas a taxa de erro entre apertar botões de plástico e configurar e girar manivelas muda drasticamente.
Por isso costuma-se dividir a história das calculadoras entre "antes das calculadoras eletrônicas" e "depois das calculadoras eletrônicas".
E a primeira das calculadoras eletrônicas veio bem antes do surgimento do microchip e chamava-se ENIAC, que eu acho que você não iria gostar de ter um em sua casa. O ENIAC era 1.000 vezes mais rápido do que as calculadoras eletromecânicas e podia conter um número decimal de até dez dígitos na memória. Isso era muito avançado para os anos 40, mas esse avanço tinha um preço (e um tamanho): 17.468 válvulas, 7.200 diodos de cristal, 1.500 relés, 70.000 resistores, 10.000 capacitores e cerca de 5 milhões de juntas soldadas a mão. Ele pesava cerca de 27 toneladas, ocupava 170 metros quadrados e consumia tanta energia quanto uma cidade pequena.

Claro que o ENIAC não foi destinado às massas, já que ele era um computador governamental, mas as bases para o cálculo moderno foram lançadas com ele e, logo, a continuidade das pesquisas e miniaturização dos componentes daria vida aos transístores. Assim as gigantescas válvulas usadas no ENIAC, que poderiam medir até 30 centímetros cada, seriam substituídas por componentes minúsculos capazes de criar uma calculadora pequena o suficiente para caber em uma mesa de escritório.
Criado em 1947, os novos transístores podiam ser alocados aos milhares em uma única placa de menos de 5 centímetros quadrados (hoje em dia, BILHÕES de transístores cabem na área de uma unha humana, por exemplo). Os transístores eram a chave para o sucesso da nova tecnologia que surgia, eram mais baratos, mais simples de serem produzidos, muito menores, mais rápidos e nem mesmo esquentavam.

O primeiro modelo dessa nova era para as calculadoras surgiu em 1961 na Inglaterra e chamava-se ANITA, um acrônimo para A New Inspiration To Arithmetic Accounting (ou, Uma nova inspiração para aritmética/contabilidade). Mas ainda havia um problema: Preço. No seu lançamento uma ANITA custava entre 350 a 400 libras, o que dá quase 9 mil dólares em dinheiro atual.
Assim você poda imaginar que elas chegaram a ser muito comuns, certo? Mas estamos chegando lá. A resposta para o problema da ANITA, inclusive, já havia até mesmo sido inventada no dia de seu lançamento.
Não demorou muito para que as pesquisas sobre transístores avançassem ao ponto de combiná-los em grandes grupos afim de otimizar os resultados. E como é o nome de um monte de transístores amontoados em uma única placa com o intuito de otimizar determinado processo? Isso mesmo, microchip.
O microchip surgiu no fim dos anos 50 e nada mais é do que uma placa que combina diversos grupos de transístores e capacitores. Assim ele pode ser mais eficiente em um espaço muito menor de hardware do que até então se tinha. A sacada para empregar os microchips em calculadoras de mesa veio somente em 1967, quando Jack Kilby, da Texas Instruments, resolveu que, com a sua ajuda, era possível baratear, diminuir e popularizar a calculadora pessoal (e ganhar muita grana com isso, é claro).

Assim, em 1967 eles lançavam a Cal Tech uma versão mais portátil (cerca de 1 kg) custando "apenas" 150 dólares (pouco mais de US$ 1.100 em valores atuais) e que fazia as 4 operações matemáticas básicas e ainda podia imprimir o resultado em uma fitinha. A empresa vendeu calculadoras como ninguém e ajudaram a popularizar a tecnologia. Em breve mais e mais produtos do dia a dia passariam a ser otimizados pelos microchips.
Do preço de mais de mil dólares para R$ 1.99 e do peso de 1 kg até algumas gramas que cabem no seu bolso, foi um pulo.

Ok, agora que já sabemos como chegamos até aqui, já podemos entender passar para a parte teórica e entender como os microchips operam o milagre de calcular 51651 vezes 218541 em milésimos de segundo.
P.S. A mesma Texas Instruments já havia criado o primeiro rádio de bolso ao substituir as válvulas pelos transístores, há mais de 10 anos antes do lançamento da Cal Tech. Todas essas revoluções foram conduzidas no Vale do Silício, e você pode conferir num post exclusivo clicando no quadradinho aqui do lado.
A base de uma calculadora (e de toda a eletrônica)
Ok, o microchip deixa o processo de fazer operações matemáticas mais rápido, MAS COMO? Calma, antes que você feche esta página por estarmos demorando para chegar no assunto principal, começarei logo a explicar o processo.
Inicialmente você precisa ter em mente um conceito bem claro em sua cabeça: Tudo na computação gira em torno de 0s e 1s, a famosa linguagem binária. Tudo mesmo.
Assim, quando você está usando o computador e digita Google no navegador, o que é processado é, na verdade, 01100111 01101111 01101111 01100111 01101100 01100101, onde cada um desses grupos de 8 dígitos representa uma letra. Inclusive, o próprio navegador e o que é exibido nele está sendo executado em uma sequência de 0 e 1 diferentes.
Como dito ali no subtítulo, 10 linhas acima, essa é a base da eletrônica. portanto serve também para os números digitados na calculadora. Nesta língua o dígito 1 vai ser 00000001, o número 2 vai ser 00000010, o 3 vai ser 00000011 e assim por diante.
E se você está se perguntando o porquê de existir a linguagem binária ou por que a linguagem binária só ter 2 estados (0 e 1), lá vem a resposta: Lembra dos transístores, que falamos há pouco? Tudo gira em torno deles.
Como você sabe, o computador (ou os seus pedaços, como processador, memória, etc.) são coisas inanimadas que não pensam. Mesmo que passemos a linguagem binária para eles, eles não vão entender os 0s e 1s; eles não sabem interpretar isso, eles não sabem que um zero é um zero. Mas há uma coisa que eles conhecem e entendem bem: eletricidade.
Assim, os transístores agem como pequenos "interruptores" de metal que servem para deixar passar a corrente elétrica, ou não deixar passar a corrente elétrica. Se a corrente passar pelo transistor A acontece alguma coisa, se não passar acontece outra. Agora multiplique isso por alguns bilhões (número de transístores no processador da sua máquina, provavelmente) e você está pronto para o funcionamento do computador; seja rodar um game, assistir um vídeo ou editar uma foto. Tudo é binário. Louco, né?
Ahh, e explicando o porquê de ser apenas 0 e 1: O motivo é que a eletricidade tem apenas 2 estágios. Ou ela está ligada ou desligada. Ponto.
Eu não deveria estar abrindo este parêntese aqui, pois isso pode complicar, mas la vai: uma nova revolução está para acontecer e tudo o que você leu até aqui está prestes a mudar.
No momento em que nos aproximamos do limite máximo de transístores embarcados em um chip (leia mais sobre a Lei de Moore clicando aqui), aumenta cada vez mais o número de computadores quânticos em operação. Por mais estranho que possa parecer, um computador quântico não opera através de linguagem binária, pois eles têm 3 estados e não apenas 2. Ao invés da corrente elétrica estar ligada ou não (como seria o normal), aqui ela pode estar ligada, desligada ou os 2 ao mesmo tempo!!
A coisa é bizarra, eu sei, mas eu não vou adentrar nesse assunto aqui neste post já que seria necessário um post completo sobre o tema para tratar de todas as suas possibilidades. Mas olha só que sorte: Este post já existe :D Se eu fosse você eu clicaria aqui para ler agora mesmo sobre computação quântica e como ela vai mudar tudo nas nossas vidas.
Como os bits viram números e são feitos os cálculos
Se você entendeu até aqui, sem mistérios, você está perto de entender como opera uma calculadora no seu mais baixo nível.
Resumidamente o esquema é o seguinte: Assim que você digita o botão correspondente ao número 2 o binário 00000010 vai para a memória, ao apertar o botão de soma o microchip identifica que ele deverá realizar uma soma de valores e, assim que o segundo valor for inserido, digamos que seja o 00000011, também conhecido como 3, o resultado da operação, 00000101, será enviado ao display, que faz o processo inverso, transforma-o em decimal e mostra o 5.

Portas lógicas
Portas-lógicas são dispositivos que recebem infinitas entradas e produzem uma única saída, sendo estas saídas "verdadeiro" ou "falso". Simples assim. A configuração para operar uma soma será uma, a configuração para gerar uma divisão é outra, etc.
Existem 7 portas lógicas diferentes, mas nós só vamos precisar entender as 4 portas básicas para decifrar como funciona uma calculadora. São elas:
- Porta AND: "And", em inglês significa "E", ou seja, caso os valores de entrada forem iguais, a saída será verdadeira. Qualquer coisa diferente disso resultará em falso.
- Porta OR: Já o "Or" em inglês, significa "ou". Assim, para que a saída seja verdadeira, pelo menos uma das entradas tem que ser verdadeiras.
- Porta XOR: Já a porta "Xor" que vem de "exclusive or" ou "ou exclusivo", só gera uma saída verdadeira caso os valores de entrada sejam diferentes.
- Porta NOT: Por último a porta "Not" que significa "não". Ela é a mais simples de todas, pois apenas inverte o valor de entrada. Se recebeu verdadeiro como entrada então a saída será falsa e vice-versa.
Mas somente as portas lógicas não dão conta do recado, afinal, as operações sempre resultarão em um "dígito extra". Para ilustrar, vamos lembrar lá da segunda série, quando você ia somar 15 e 25, por exemplo. Naquela época você não fazia o cálculo de cabeça e então fazia o processo conforme o figurino: colocava um número sobre o outro e então começava a somar da direita para a esquerda. Primeiro somava o 5 do 15 com o 5 do 25. O resultado é 10, então o 0 vai lá embaixo e o 1 "sobe" para ser somado com os valores à esquerda, neste caso o 1 e o 2, certo? Pois bem, esse 1 sendo transportado entre o cálculo é a função do adder em uma operação binária. Repare que em binários só temos 2 possibilidades: 0 ou 1. E somar o binário 1 com outro binário 1 já excede o limite de possibilidades. Por isso que nesse caso o resultado é 0 e um 1 é carregado para ser incorporado à próxima operação, à esquerda. Esse 1 que "sobe" em operações binárias é chamado de "carry", que vem do inglês "carregar". O GIF abaixo mostra uma soma em binário acontecendo. Os adders existem em duas formas: Full adder e half adder, sendo este segundo o mais utilizado e mais comum nos exemplos que veremos abaixo, em breve. Agora é só pegar tudo, misturar diferentes combinações entre essas quatro portas lógicas com um half adder e você vai ter um dispositivo capaz de fazer cálculos. Entendida a teoria, podemos passar aos exemplos de circuitos lógicos, mas antes uma importante observação: os circuitos abaixo NÃO SÃO A ÚNICA OPÇÃO de fazer as operações. As coisas podem variar bastante dependendo da complexidade da calculadora, tamanho do hardware, etc. etc. Por ser a operação mais comum, explicarei a soma de binários em maiores detalhes, com todo o passo a passo necessário. Os demais serão explicados sem tanta "enrolação". Voltando às tabelas verdade vistas acima, peguemos a porta lógica Xor que é a base de uma operação de soma e apliquemos o conceito de carry, ou seja, do "número que sobe". Assim as possibilidades de uma porta xor aplicadas à soma de binário são as seguintes: Logo, ele será representado da maneira que você vê abaixo, já contando com o carry (ou adder) para trabalhar com o número que sobe.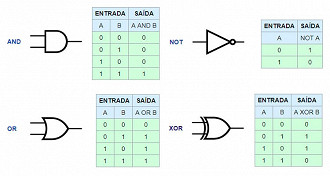
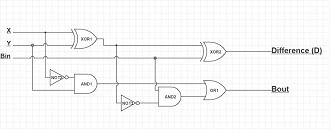
Adders
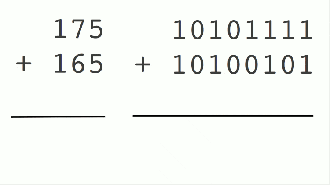
Soma de binários
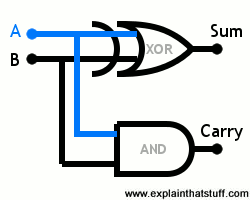
No exemplo ao lado estamos inserindo dois números binários para serem somados (A e B). Eles "viajam" simultaneamente para as entradas das duas portas lógicas - uma porta xor na parte superior e uma porta and abaixo que funciona como adder. A saída da porta xor dá a soma das duas entradas, enquanto que a saída da porta and nos diz se precisamos subir um 1 ou não. depois o processo é repetido até que não haja mais binários a serem somados e o valor final seja obtido.
Para ficar mais vamos pegar as quatro possibilidades de saída de uma porta xor e simular uma saída:
- Se A e B recebem um zero, estamos fazendo a soma 0 + 0 = 0. Assim a porta xor resultará em zero e a porta and também (lembre-se que para dar saída 1 em porta and você precisa que as duas entradas sejam 1). Portanto, neste caso o resultado da nossa soma é zero e o carry é também zero.
- Se A recebe um 0 e B recebe 1, estamos fazendo a soma 0 + 1 = 1. A porta xor dá 1 se qualquer uma (mas não ambas) de suas entradas é 1. A porta and dá 1 apenas se ambas as entradas forem 1. Então o resultado da nossa soma é 1 e o carry é zero.
- Se A recebe 1 e B recebe um 0, é o mesmo que no exemplo anterior: o resultado de nossa soma é 1 e o carry é 0.
- Finalmente, se A e B receberem 1, estamos fazendo a soma 1 + 1 = 2. Agora a porta xor dá 0, enquanto a porta and dá 1. Portanto, a soma é 0 e o carry é 1, o que significa que o resultado final é 10 em binário ou 2 em decimal.
Subtração de binários
Para fazer uma subtração o processo é parecido com a soma, porém tem um elemento adicional de suma importância: a porta not.
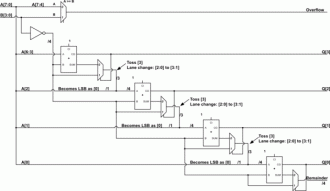
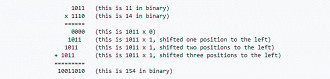
Uma das formas de montar o circuito pode ser vista ao lado. Neste modelo foi usado um half adder, montando-se assim um circuito mais simples, porém mais limitado. Repare que é possível o cálculo de X - Y, mas não é possível o cálculo de Y - X. Tudo por conta do not estar presente só em um lado da operação. Para resolver isso poderia ser usado um full adder, que deixaria o processo mais complexo, como você pode ver abaixo. Já com a multiplicação será feita da seguinte forma: Digamos que nossa conta seja 8 vezes 14. Em binários o 8 é 1011 e o 14 é 1110. Assim, para multiplicarmos 1011 por 1110 iremos pegar o número de cima (1011) e multiplicar por cada dígito de 1110, da direita para a esquerda. Os resultados são colocados um abaixo do outro, deslocando uma casa para a esquerda a cada novo valor. E para gerar estes resultados não tem mistério não. Apenas multiplique normalmente. Quando for multiplicado por 0 o resultado é 0 e quando for multiplicado por 1 é 1. Simples. Abaixo um exemplo de como ela funciona na prática. No final é feito uma soma de binários, assim como fazemos uma soma após executar a multiplicação dos dígitos no nosso modo decimal tradicional que aprendemos na escola. A multiplicação, aliás, é o método mais fácil e similar ao que estamos acostumados. Um dos circuitos possíveis para a multiplicação pode ser visto abaixo, onde são multiplicados 2 valores de 2 bits cada. E, para fechar, a divisão de binários acontece de maneira similar ao modo decimal, com a diferença de que você deve atentar ao modo como subtrai quando for apurar o resto da divisão, já que precisa empregar a subtração de binários, é claro. Um dos possíveis circuitos lógicos para uma divisão seria: Bom, ao menos que você esteja cursando algum curso de eletrônica, engenharia ou ciência da computação, aqui está uma boa base sobre como uma calculadora funciona. Resumindo: Tudo é feito a partir de um determinado número de portas lógicas AND, OR, XOR e NOT contidas dentro de chips que estão conectados entre si. Organize tudo isso em uma placa e você terá uma calculadora. P.S. Reafirmo: Claro que podemos usar outros circuitos, inclusive outras portas lógicas, mas aprofundar-se nesse tópico fica por conta de quem tiver interesse. Se este é o seu aso, abaixo seguem bons link. Para saber mais: Vintage Calculators, The Calculator Site, Energia Inteligente, USCS Electronic Music Studios, Explain That Stuff, Learn About Electronics, Exploring Binary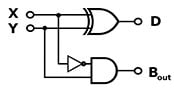
O segredo da subtração está no not
Multiplicação de binários
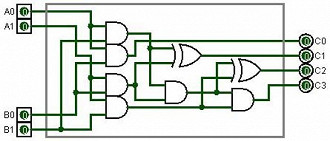
Divisão de binários